Extensions to Higher-Dimensions of an Unconditionally Stable ADE Scheme for the Convection-Diffusion Equation
Résumé
An unconditionally stable alternating direction explicit scheme (ADE) to solve the one-dimensional unsteady convection-diffusion equation was developed by J. Xie, Z. Lin and J. Zhou in [6]. Aside from being explicit and unconditionally stable, the method is straightforward to implement. In this paper we show extensions of this scheme to higher-dimensions of the convection-diffusion equation subject to Dirichlet boundary conditions. By expressing the equation with a local series expansion over a rectangular grid, a linear system of symbolic equations is obtained which is tedious to solve for manually and we addressed this challenge using symbolic computation. The solutions obtained are explicit closed-form formulas which are then used to iteratively solve the unsteady convectiondiffusion equation by traversing the discrete grid in an alternating direction fashion. Finally, extensions to higher dimensions can be easily deduced from the 2D formulas. We conclude the paper with numerical simulation results for diffusion and convection-diffusion problems compared to analytical solutions showing the performance of the method and its numerical stability.
Fichier principal
 GuayColinEgli_ADE_TechRep.pdf (1.31 Mo)
Télécharger le fichier
GuayColinEgli_ADE_TechRep.pdf (1.31 Mo)
Télécharger le fichier
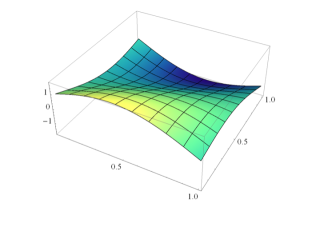 InitialDEqn.png (94.87 Ko)
Télécharger le fichier
InitialDEqn.png (94.87 Ko)
Télécharger le fichier
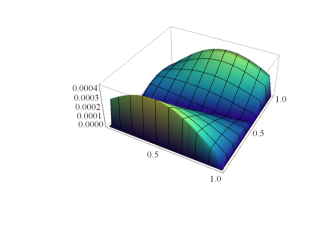 ErrorDEqn.png (113.11 Ko)
Télécharger le fichier
ErrorDEqn.png (113.11 Ko)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Format : Figure, Image