| HAL-Inria | Publications, software ... of Inria's scientists |
Poster communications
The Maximum Degree of a Random Delaunay Triangulation in a Smooth Convex
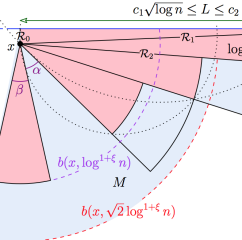
Abstract : We give a new polylogarithmic bound on the maximum degree of a random Delaunay triangulation in a smooth convex, that holds with probability one as the number of points goes to infinity. In particular, our new bound holds even for points arbitrarily close to the boundary of the domain.
Cited literature [4 references]
https://hal.inria.fr/hal-01018187
Contributor : Ross Hemsley <>
Submitted on : Thursday, July 3, 2014 - 5:34:49 PM
Last modification on : Friday, May 25, 2018 - 12:02:03 PM
Document(s) archivé(s) le : Friday, October 3, 2014 - 12:01:23 PM
Contributor : Ross Hemsley <>
Submitted on : Thursday, July 3, 2014 - 5:34:49 PM
Last modification on : Friday, May 25, 2018 - 12:02:03 PM
Document(s) archivé(s) le : Friday, October 3, 2014 - 12:01:23 PM
Files
degree.pdf
Publisher files allowed on an open archive
- poster.pdf Publisher files allowed on an open archive