Analysis of Farthest Point Sampling for Approximating Geodesics in a Graph
Résumé
A standard way to approximate the distance between two vertices $p$ and $q$ in a graph is to compute a shortest path from $p$ to $q$ that goes through one of $k$ sources, which are well-chosen vertices. Precomputing the distance between each of the $k$ sources to all vertices yields an efficient computation of approximate distances between any two vertices. One standard method for choosing $k$ sources is the so-called Farthest Point Sampling (FPS), which starts with a random vertex as the first source, and iteratively selects the farthest vertex from the already selected sources.
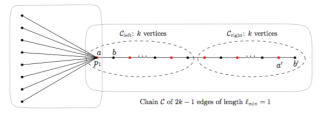
In this paper, we analyze the stretch factor $\mathcal{F}_{\text{FPS}}$ of approximate geodesics computed using FPS, which is the maximum, over all pairs of distinct vertices, of their approximated distance over their geodesic distance in the graph. We show that $\mathcal{F}_{\text{FPS}}$ can be bounded in terms of the minimal value $\mathcal{F}^\ast$ of the stretch factor obtained using an optimal placement of $k$ sources as $\mathcal{F}_{\text{FPS}}\leq 2 r_e^2 \mathcal{F}^\ast+ 2 r_e^2 + 8 r_e + 1$, where $r_e$ is the length ratio of longest edge over the shortest edge in the graph. We further show that the factor $r_e$ is not an artefact of the analysis by providing a class of graphs for which $\mathcal{F}_{\text{FPS}} \geq \frac{1}{2} r_e \mathcal{F}^\ast$.
In this paper, we analyze the stretch factor $\mathcal{F}_{\text{FPS}}$ of approximate geodesics computed using FPS, which is the maximum, over all pairs of distinct vertices, of their approximated distance over their geodesic distance in the graph. We show that $\mathcal{F}_{\text{FPS}}$ can be bounded in terms of the minimal value $\mathcal{F}^\ast$ of the stretch factor obtained using an optimal placement of $k$ sources as $\mathcal{F}_{\text{FPS}}\leq 2 r_e^2 \mathcal{F}^\ast+ 2 r_e^2 + 8 r_e + 1$, where $r_e$ is the length ratio of longest edge over the shortest edge in the graph. We further show that the factor $r_e$ is not an artefact of the analysis by providing a class of graphs for which $\mathcal{F}_{\text{FPS}} \geq \frac{1}{2} r_e \mathcal{F}^\ast$.
Fichier principal
 ShortestPaths_final.pdf (322.34 Ko)
Télécharger le fichier
ShortestPaths_final.pdf (322.34 Ko)
Télécharger le fichier
 2016 Farthest Point Sampling.png (43.74 Ko)
Télécharger le fichier
2016 Farthest Point Sampling.png (43.74 Ko)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Loading...