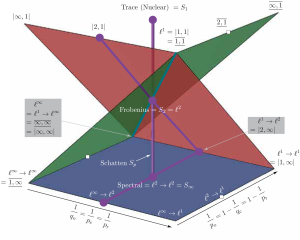
This is the first paper of a two-long series in which we study linear generalized inverses that minimize matrix norms. Such generalized inverses are famously represented by the Moore-Penrose pseudoinverse (MPP) which happens to minimize the Frobenius norm. Freeing up the degrees of freedom associated with Frobenius optimality enables us to promote other interesting properties. In this Part I, we look at the basic properties of norm-minimizing generalized inverses, especially in terms of uniqueness and relation to the MPP. We first show that the MPP minimizes many norms beyond those unitarily invariant, thus further bolstering its role as a robust choice in many situations. We then concentrate on some norms which are generally not minimized by the MPP, but whose minimization is relevant for linear inverse problems and sparse representations. In particular, we look at mixed norms and the induced $\ell^p \rightarrow \ell^q$ norms. An interesting representative is the sparse pseudoinverse which we study in much more detail in Part II. Next, we shift attention from norms to matrices with interesting behaviors. We exhibit a class whose generalized inverse is always the MPP—even for norms that normally result in different inverses—and a class for which many generalized inverses coincide, but not with the MPP. Finally, we discuss efficient computation of norm-minimizing generalized inverses.