Covering families of triangles
Résumé
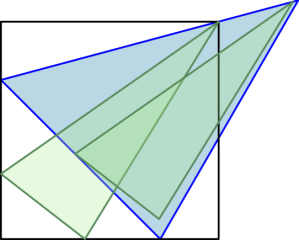
A cover for a family $\mathcal{F}$ of sets in the plane is a set into which every set in $\mathcal{F}$ can be isometrically moved. We are interested in the convex cover of smallest area for a given family of triangles. Park and Cheong conjectured that any family of triangles of bounded diameter has a smallest convex cover that is itself a triangle. The conjecture is equivalent to the claim that for every convex set $\mathcal{X}$ there is a triangle $Z$ whose area is not larger than the area of $\mathcal{X}$, such that $Z$ covers the family of triangles contained in $\mathcal{X}$. We prove this claim for the case where a diameter of~$\mathcal{X}$ lies on its boundary. We also give a complete characterization of the smallest convex cover for the family of triangles contained in a half-disk, and for the family of triangles contained in a square. In both cases, this cover is a triangle.
Une couverture pour une famille $\mathcal{F}$ d'ensembles du plan est un ensemble dans lequel chaque ensemble de $\mathcal{F}$ peut être déplacé de manière isométrique. Nous nous intéressons à la couverture convexe ayant la plus petite surface pour une famille de triangles. Park et Cheong ont supposé que toute famille de triangles de diamètre borné a une plus petite couverture convexe qui est elle-même un triangle. Cette conjecture est équivalente à l'affirmation selon laquelle pour chaque ensemble convexe $\mathcal{X}$ il y a un triangle $Z$ dont la surface n'est pas plus grande que celle de $\mathcal{X}$, de sorte que $Z$ couvre la famille de triangles contenus dans $\mathcal{X}$. Nous prouvons cette affirmation dans le cas où un diamètre de $\mathcal{X}$ se trouve sur le bord de $\mathcal{X}$. Nous donnons également une caractérisation complète de la plus petite couverture convexe pour la famille de triangles contenus dans un demi-disque, et pour la famille de triangles contenus dans un carré.
Fichier principal
 RR-9378.pdf (4.43 Mo)
Télécharger le fichier
RR-9378.pdf (4.43 Mo)
Télécharger le fichier
 vignette.png (43.13 Ko)
Télécharger le fichier
Maple-computations.zip (73.25 Ko)
Télécharger le fichier
vignette.png (43.13 Ko)
Télécharger le fichier
Maple-computations.zip (73.25 Ko)
Télécharger le fichier
Format : Figure, Image