Lines tangent to four triangles in three-dimensional space
Résumé
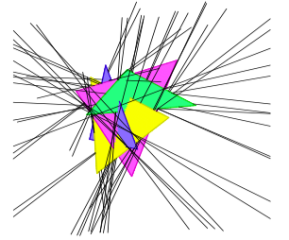
We investigate the lines tangent to four triangles in $\mathbb{R}^3$. By a construction, there can be as many as 62 tangents. We show that there are at most 162 connected components of tangents, and at most 156 if the triangles are disjoint. In addition, if the triangles are in (algebraic) general position, then the number of tangents is finite and it is always even.
Domaines
Géométrie algorithmique [cs.CG]
Fichier principal
 triangles_hal.pdf (497.43 Ko)
Télécharger le fichier
triangles_hal.pdf (497.43 Ko)
Télécharger le fichier
 2007 Lines tangent to four triangles.png (59.11 Ko)
Télécharger le fichier
2007 Lines tangent to four triangles.png (59.11 Ko)
Télécharger le fichier
Format : Figure, Image
Loading...