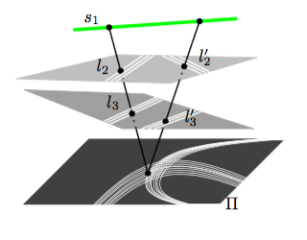
Résumé : Computing shadow boundaries is a difficult problem in the case of non-point light sources. A point is in the umbra if it does not see any part of any light source; it is in full light if it sees entirely all the light sources; otherwise, it is in the penumbra. While the common boundary of the penumbra and the full light is well understood, less is known about the boundary of the umbra. In this paper we prove various bounds on the complexity of the umbra and the penumbra cast on a fixed plane by a segment or convex polygonal light source in the presence of convex polygonal or polyhedral obstacles in $\mathbb{R}^3$. In particular, we show that a single segment light source may cast on a plane, in the presence of two disjoint triangles, four connected components of umbra and that two fat convex and disjoint obstacles of total complexity $n$ can give rise to as many as $\Omega(n)$ connected components of umbra. In a scene consisting of a segment light source and $k$ disjoint convex polyhedra of total complexity $n$, we prove an $\Omega(nk^2+k^4)$ lower bound on the maximum number of connected components of the umbra and a $O(nk^3)$ upper bound on its complexity; if the obstacles may intersect, we only prove an upper bound of $O(n^2k^2)$. We also prove that, in the presence of $k$ convex polyhedra of total complexity $n$, some of which are light sources, the umbra cast on a plane may have in the worst case $\Omega(n^2k^3 + nk^5)$ connected components and has complexity $O(n^3k^3)$ (the polyhedra are supposed pairwise disjoint for lower bounds and possibly intersecting for the upper bounds). These are the first bounds on the size of the umbra in terms of both $k$ and $n$. These results prove that the umbra, which is bounded by arcs of conics, is intrinsically much more intricate than the boundary between full light and penumbra which is bounded by line segments and whose worst-case complexity is, as we show, in $\Omega(nk +k^4)$ and $O(nk\alpha(k) +k^4)$; moreover, if there are only $O(1)$ light sources of total complexity $m$, then the complexity is in $\Omega(n\alpha(k) +km +k^2)$ and $O(n\alpha(k) +km\alpha(k) +k^2)$.