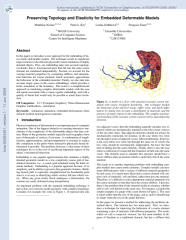
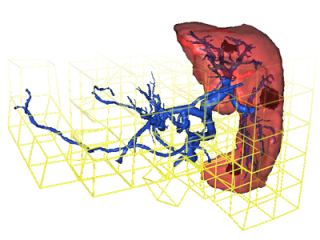
Preserving Topology and Elasticity for Embedded Deformable Models
Résumé
In this paper we introduce a new approach for the embedding of linear elastic deformable models. Our technique results in significant improvements in the efficient physically based simulation of highly detailed objects. First, our embedding takes into account topological details, that is, disconnected parts that fall into the same coarse element are simulated independently. Second, we account for the varying material properties by computing stiffness and interpolation functions for coarse elements which accurately approximate the behaviour of the embedded material. Finally, we also take into account empty space in the coarse embeddings, which provides a better simulation of the boundary. The result is a straightforward approach to simulating complex deformable models with the ease and speed associated with a coarse regular embedding, and with a quality of detail that would only be possible at much finer resolution.
Fichier principal
 composite.pdf (4.82 Mo)
Télécharger le fichier
composite.pdf (4.82 Mo)
Télécharger le fichier
 liver.png (132.02 Ko)
Télécharger le fichier
liver.png (132.02 Ko)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Loading...