Subdivision Invariant Polynomial Interpolation
Résumé
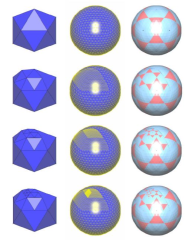
In previous works a polynomial interpolation method for triangular meshes has been introduced. This interpolant can be used to design smooth surfaces of arbitrary topological type. In a design process, it is very useful to be able to locate the deformation made on a geometric model. The previously introduced interpolant has the so-called strict locality property: when a mesh vertex is changed, only the surface patches containing this vertex are changed. This enables to locate the deformation at the size of the input triangles. Unfortunately this is not sufficient if the designer wants to add some detail at a smaller size than that of the input triangles. In this paper, we propose a modification of our interpolant, that enables to arbitrary refine the input triangulation, without changing the resulting surface. We call this property the subdivision invariance. After refinement of the input triangulation, the modification of one of the vertices will change the shape of the interpolant at the scale of the refined triangulation. In this way, it is possible to add details at an arbitrary fine scale.
Fichier principal
 paper-vismath2.pdf (937.99 Ko)
Télécharger le fichier
paper-vismath2.pdf (937.99 Ko)
Télécharger le fichier
 IMG01.jpg (53.18 Ko)
Télécharger le fichier
IMG01.jpg (53.18 Ko)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Loading...