Covering spaces and Delaunay triangulations of the 2D flat torus - Archive ouverte HAL Access content directly
Conference Papers Year : 2012

Covering spaces and Delaunay triangulations of the 2D flat torus

(1) , (1) , (2)
1
2

Abstract

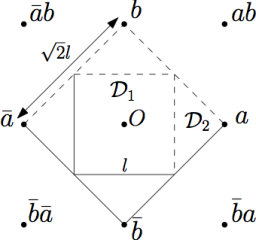
A previous algorithm was computing the Delaunay triangulation of the flat torus, by using a 9-sheeted covering space. We propose a modification of the algorithm using only a 8-sheeted covering space, which allows to work with 8 periodic copies of the input points instead of 9. The main interest of our contribution is not only this result, but most of all the method itself: this new construction of covering spaces generalizes to Delaunay triangulations of surfaces of higher genus.

Domains

Computer Science [cs] Computational Geometry [cs.CG]
Vignette du fichier
2-sh.png (16.93 Ko) Télécharger le fichier Fichier principal
Vignette du fichier
hal.pdf (309.21 Ko) Télécharger le fichier
Format : Figure, Image
Origin : Files produced by the author(s)
Origin : Files produced by the author(s)

Monique Teillaud  : Connect in order to contact the contributor

https://hal.inria.fr/hal-01109626

Submitted on : Monday, January 26, 2015-4:15:55 PM

Last modification on : Saturday, June 25, 2022-9:09:21 PM

Long-term archiving on: Monday, April 27, 2015-10:45:57 AM

Download

Dates and versions

hal-01109626 , version 1 (26-01-2015)

Identifiers

  • HAL Id : hal-01109626 , version 1

Cite

Mikhail Bogdanov, Monique Teillaud, Gert Vegter. Covering spaces and Delaunay triangulations of the 2D flat torus. 28th European Workshop on Computational Geometry, Mar 2012, Assisi, Italy. ⟨hal-01109626⟩

Export

BibTeX TEI Dublin Core DC Terms EndNote Datacite

Collections

INRIA INRIA2
188 View
179 Download

Share

Gmail Facebook Twitter LinkedIn More