Parabolic-cylindrical moving least squares surfaces
Résumé
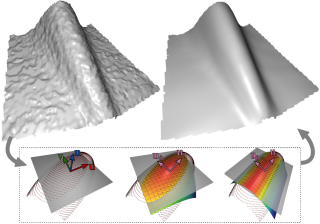
Moving least squares (MLS) surface approximation is a popular tool for the processing and reconstruction of non-structured and noisy point clouds. This paper introduces a new variant improving the approximation quality when the underlying surface is assumed to be locally developable, which is often the case in point clouds coming from the acquisition of manufactured objects. Our approach follows Levin's classical MLS procedure: the point cloud is locally approximated by a bivariate quadratic polynomial height-field defined in a local tangent frame. The a priori developability knowledge is introduced by constraining the fitted poly-nomials to have a zero-Gaussian curvature leading to the actual fit of so-called parabolic cylinders. When the local developability assumption cannot be made unambiguously, our fitted parabolic cylinders seamlessly degenerate to linear approximations. We show that our novel MLS kernel reconstructs more locally-developable surfaces than previous MLS methods while being faithful to the data.
Fichier principal
 main.pdf (19.21 Mo)
Télécharger le fichier
main.pdf (19.21 Mo)
Télécharger le fichier
 graphical_abstract.jpg (166.13 Ko)
Télécharger le fichier
graphical_abstract.jpg (166.13 Ko)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Origine : Fichiers produits par l'(les) auteur(s)
Commentaire : Graphical abstract
Origine : Fichiers produits par l'(les) auteur(s)
Commentaire : Graphical abstract
Loading...