Fast and rigorous arbitrary-precision computation of Gauss-Legendre quadrature nodes and weights
Résumé
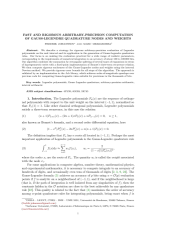
We describe a strategy for rigorous arbitrary-precision evaluation of Legendre polynomials on the unit interval and its application in the generation of Gauss-Legendre quadrature rules. Our focus is on making the evaluation practical for a wide range of realistic parameters, corresponding to the requirements of numerical integration to an accuracy of about 100 to 100 000 bits. Our algorithm combines the summation by rectangular splitting of several types of expansions in terms of hypergeometric series with a fixed-point implementation of Bonnet's three-term recurrence relation. We then compute rigorous enclosures of the Gauss-Legendre nodes and weights using the interval Newton method. We provide rigorous error bounds for all steps of the algorithm. The approach is validated by an implementation in the Arb library, which achieves order-of-magnitude speedups over previous code for computing Gauss-Legendre rules with simultaneous high degree and precision.
Fichier principal
 legendre.pdf (734.85 Ko)
Télécharger le fichier
benchplot.pdf (135.38 Ko)
Télécharger le fichier
timeplot.pdf (73.07 Ko)
Télécharger le fichier
legendre.pdf (734.85 Ko)
Télécharger le fichier
benchplot.pdf (135.38 Ko)
Télécharger le fichier
timeplot.pdf (73.07 Ko)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Origine : Fichiers produits par l'(les) auteur(s)
Loading...