Walking in a Planar Poisson-Delaunay Triangulation: Shortcuts in the Voronoi Path
Résumé
Let $X_n$ be a planar
Poisson point process of intensity $n$.
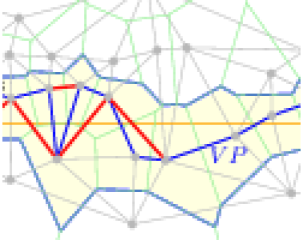
We give a new proof that the expected length of the Voronoi path between $(0,0)$ and $(1,0)$ in
the Delaunay triangulation associated with $X_n$
is $\tfrac{4}{\pi}\simeq 1.27$ when $n$ goes to infinity;
and we also prove that the variance of this length is $\Theta(1/\sqrt{n})$.
We investigate the length of possible shortcuts in this path,
and define a shortened Voronoi path whose expected length
can be expressed as an integral that is numerically evaluated to
$\simeq 1.16$.
The shortened Voronoi path has the property to be {\em locally defined};
and is shorter than the previously known locally defined paths in
Delaunay triangulation such as
the upper path whose expected length is $35/3\pi^2\simeq 1.18$.
Domaines
Géométrie algorithmique [cs.CG]
Fichier principal
 paper.pdf (844.11 Ko)
Télécharger le fichier
paper.pdf (844.11 Ko)
Télécharger le fichier
 vignette.png (15.37 Ko)
Télécharger le fichier
vignette.png (15.37 Ko)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Loading...