Gaussian mixture learning from noisy data
Résumé
We address the problem of learning a Gaussian mixture from a set of noisy data points. Each input point has an associated covariance matrix that can be interpreted as the uncertainty by which this point was observed. We derive an EM algorithm that learns a Gaussian mixture that minimizes the Kullback-Leibler divergence to a variable kernel density estimator on the input data. The proposed algorithm performs iterative optimization of a strict bound on the Kullback-Leibler divergence, and is provably convergent.
Domaines
Apprentissage [cs.LG]
Fichier principal
 verbeek04tr.pdf (86.51 Ko)
Télécharger le fichier
verbeek04tr.pdf (86.51 Ko)
Télécharger le fichier
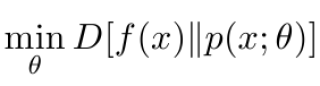 VV04.png (6.11 Ko)
Télécharger le fichier
VV04.png (6.11 Ko)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Loading...