Explicit construction of chaotic attractors in Glass networks
Résumé
Chaotic dynamics have been observed in example piecewise-affine models of gene regulatory networks. Here we show how the underlying Poincaré maps can be explicitly constructed. To do this, we proceed in two steps. First, we consider a limit case, where some parameters tend to ∞, and then consider the case with finite parameters as a perturbation of the previous one. We provide a detailed example of this construction, in 3-d, with several thresholds per variable. This construction is essentially a topological horseshoe map. We show that the limit situation is conjugate to the golden mean shift, and is thus chaotic. Then, we show that chaos is preserved for large parameters, relying on the structural stability of the return map in the limit case. We also describe a method to embed systems with several thresholds into binary systems, of higher dimensions. This shows that all results found for systems having several thresholds remain valid in the binary case.
Domaines
Modélisation et simulation
Fichier principal
 Horseshoe_final.pdf (857.61 Ko)
Télécharger le fichier
Horseshoe_final.pdf (857.61 Ko)
Télécharger le fichier
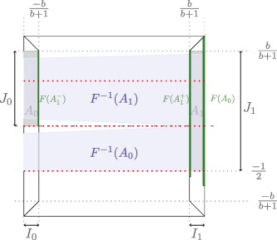 im1.jpg (17.55 Ko)
Télécharger le fichier
im1.jpg (17.55 Ko)
Télécharger le fichier
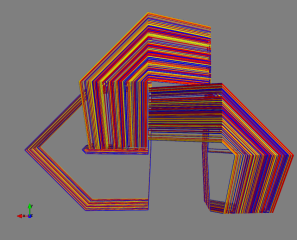 3traj2.png (287.97 Ko)
Télécharger le fichier
3traj2.png (287.97 Ko)
Télécharger le fichier
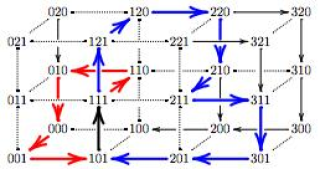 edwards12.jpg (11.66 Ko)
Télécharger le fichier
edwards12.jpg (11.66 Ko)
Télécharger le fichier
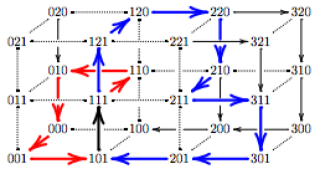 edwards12.png (21.96 Ko)
Télécharger le fichier
edwards12.png (21.96 Ko)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Origine : Fichiers produits par l'(les) auteur(s)
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Origine : Fichiers produits par l'(les) auteur(s)
Origine : Fichiers produits par l'(les) auteur(s)
Loading...