FeaStNet: Feature-Steered Graph Convolutions for 3D Shape Analysis
Résumé
Convolutional neural networks (CNNs) have massively impacted visual recognition in 2D images, and are now ubiquitous in state-of-the-art approaches. CNNs do not easily extend, however, to data that are not represented by regular grids, such as 3D shape meshes or other graph-structured data, to which traditional local convolution operators do not directly apply. To address this problem, we propose a novel graph-convolution operator to establish correspondences between filter weights and graph neighborhoods with arbitrary connectivity. The key novelty of our approach is that these correspondences are dynamically computed from features learned by the network, rather than relying on predefined static coordinates over the graph as in previous work. We obtain excellent experimental results that significantly improve over previous state-of-the-art shape correspondence results. This shows that our approach can learn effective shape representations from raw input coordinates, without relying on shape descriptors.
Fichier principal
 2589+supp.pdf (42.82 Mo)
Télécharger le fichier
2589+supp.pdf (42.82 Mo)
Télécharger le fichier
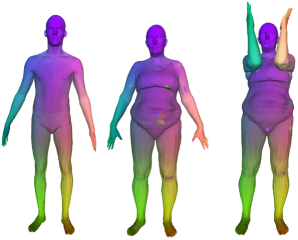 FeastNetHal.png (285.15 Ko)
Télécharger le fichier
FeastNetHal.jpg (59.78 Ko)
Télécharger le fichier
FeastNetHal.png (285.15 Ko)
Télécharger le fichier
FeastNetHal.jpg (59.78 Ko)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Loading...