Dynamic Triangulation of Implicit Surfaces: towards the handling of topology changes
Résumé
In this paper, we introduce a new approach to mesh an animated implicit surface for rendering purposes. This approach is based on a double triangulation of the surface. In the first triangulation, the vertices are the nodes of a finite element model. The aim of this model is to uniformly and dynamically sample the surface. It is robust, efficient and prevents the inversion of triangles. The second triangulation is dynamically created from the first one at each frame and provides details in regions of high curvature. Lastly, we present a mechanism to deal with both the topological merging and splitting of surfaces. As shown in our results, our approach provides robust, quality, interactive rendering of animated implicit surfaces, including those with certain kinds of topology changes.
Fichier principal
 RR-6128.pdf (772.82 Ko)
Télécharger le fichier
RR-6128.pdf (772.82 Ko)
Télécharger le fichier
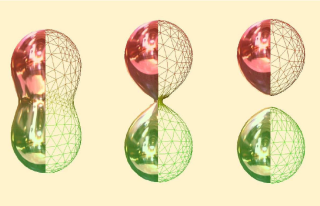 0.jpg (107.91 Ko)
Télécharger le fichier
0.jpg (107.91 Ko)
Télécharger le fichier
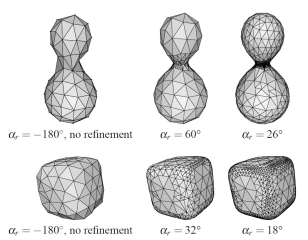 fig09.jpg (152.16 Ko)
Télécharger le fichier
fig09.jpg (152.16 Ko)
Télécharger le fichier
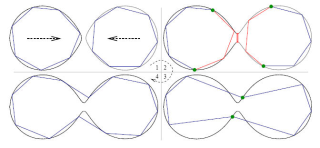 fig11.jpg (36.58 Ko)
Télécharger le fichier
fig11.jpg (36.58 Ko)
Télécharger le fichier
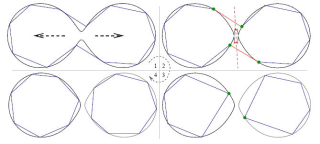 fig12.jpg (36.91 Ko)
Télécharger le fichier
fig12.jpg (36.91 Ko)
Télécharger le fichier
 fig13a.jpg (22.85 Ko)
Télécharger le fichier
fig13a.jpg (22.85 Ko)
Télécharger le fichier
 fig13b.jpg (38.56 Ko)
Télécharger le fichier
fig13b.jpg (38.56 Ko)
Télécharger le fichier
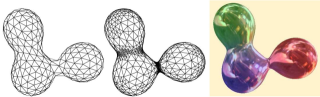 fig14a.jpg (88.85 Ko)
Télécharger le fichier
fig14a.jpg (88.85 Ko)
Télécharger le fichier
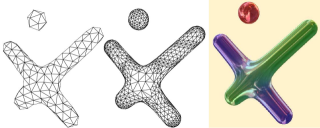 fig14b.jpg (90.51 Ko)
Télécharger le fichier
fig14b.jpg (90.51 Ko)
Télécharger le fichier
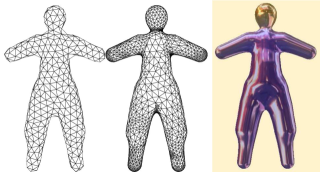 fig14c.jpg (141.12 Ko)
Télécharger le fichier
fig14c.jpg (141.12 Ko)
Télécharger le fichier
 merge_split.jpg (190.57 Ko)
Télécharger le fichier
rr6128.avi (54.1 Mo)
Télécharger le fichier
merge_split.jpg (190.57 Ko)
Télécharger le fichier
rr6128.avi (54.1 Mo)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Vidéo
Loading...